Optimization

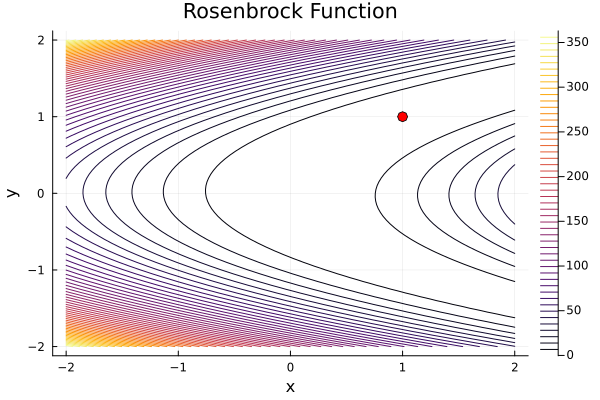
Nonlinear optimization, also known as nonlinear programming (NLP), is a branch of mathematical optimization that deals with optimizing objective functions subject to nonlinear constraints. In nonlinear optimization, both the objective function and the constraints can involve nonlinear relationships and functions. The goal is to find the values of decision variables that optimize (minimize or maximize) the objective function while satisfying the constraints.

Soliton

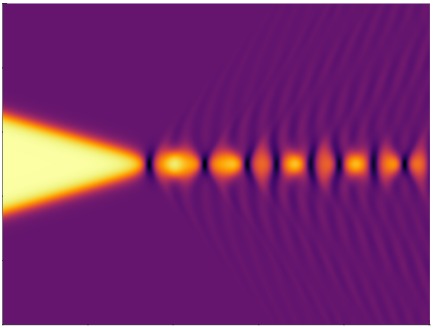
Solitons are a fascinating concept in mathematics and physics that describe special types of nonlinear waves or wave-like solutions that maintain their shape and energy as they propagate through a medium. They were first discovered in the context of fluid dynamics but have since found applications in various fields, including particle physics, optics, and nonlinear optics, condensed matter physics, and even biology.

Packing Problem

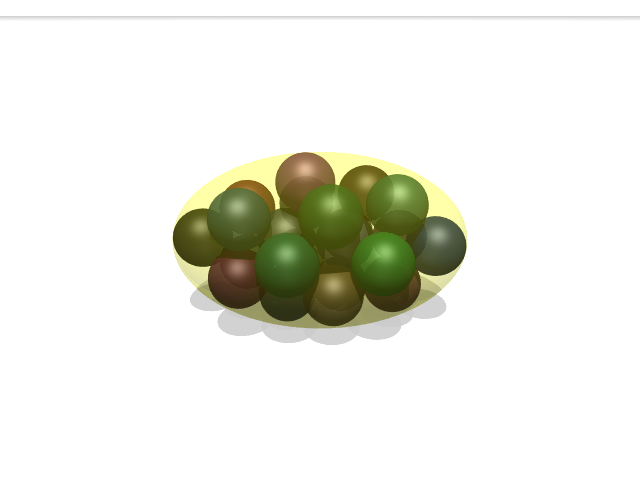
Packing problems are a class of mathematical and computational optimization problems that involve arranging objects (usually of specific shapes and sizes) within a defined space in the most efficient or optimal way possible. These problems have practical applications in various fields, including logistics, manufacturing, cutting, and layout design. There are several types of packing problems, each with its own set of rules and objectives. Here are some common packing problems: Rectangular Packing Problem, Circle Packing Problem, Irregular Shape Packing, Knapsack Problem.